中山大學現代遠程教育入學考試《數學》（高中起點升專科）
考試大綱

 
總 要 求
考生應理解和掌握中學數學基礎知識、基本技能、基本方法，應注意各部分知識結構及知識間的內在聯系。考查邏輯思維能力、運算能力、空間想象能力，以及運用所學數學知識和方法分析問題和解決問題的能力。為后繼課程的學習作準備。
考試內容的知識要求和能力要求作如下說明：
    1、知識要求
    本大綱對所列知識提出了三個層次的不同要求，三個層次由低到高順序排列，且高一級層次要求包含低一級要求。三個層次分別為：
    了解：要求考生對所列知識的含義有初步的認識，識記有關內容，并能進行直接運用。
    理解、掌握、會：要求考生對所列知識的含義有較深的認識，能夠解釋、舉例或變形、推斷，并能運用知識解決有關問題。
    靈活運用：要求考生對所列知識能夠綜合運用，并能解決較為復雜的數學問題。
   2、能力要求
    邏輯思維能力：會對問題進行觀察、比較、分析、綜合、抽象與概括；會用演繹、歸納和類比進行推理；能準確、清晰、有條理地進行表述。
    運用能力：理解算理，會根據法則、公式、概念進行數、式、方程的正確運算和變形；能分析條件，尋求與設計合理、簡捷的運算途徑；能根據要求對數據進行估計，能運用計算器進行數值計算。
    空間想象能力：能根據條件畫出圖形，根據圖形想象出直觀形象；能正確地分析出圖形中基本元素及其相互關系；能對圖形進行分解、組合、變形。
    分析問題和解決問題的能力：能閱讀理解對問題進行陳述的材料；能綜合應用所學數學知識、思想和方法解決問題，包括解決在相關學科、生產、生活中的數學問題，并能用數學語言正確地加以表述。

• 復習考試內容

第一部分 代 數
（一）函數

1. 了解集合的意義及其表示方法。了解空集、全集、子集、交集、并集、補集的概念及表示方法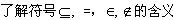，，并能運用這些符號表示集合、元素與集合的關系。
2. 理解函數概念，會求一些常見函數的定義域。
3. 理解函數的單調性和奇偶性的概念，掌握增函數、減函數、減函數及奇函數、偶函數的圖像特征。
4. 理解一次函數、反比例函數的概念，掌握它們的圖像和性質，會求它們的解析式。
5. 理解二次函數的概念，掌握它的圖像和性質以及函數 y=aχ²+bχ+c(a≠0)與y=aχ² (a≠0)的圖像間的關系；會求二次函數的解析式及最大值或最小值。能靈活運用二次函數的知識解決有關問題。
6. 了解反函數的意義。會求一些簡單函數的反函數。

7、理解指數函數、對數函數的概念，掌握它們的圖像和性質，會用它們解決有關問題。
（二）不等式和不等式組

1. 理解不等式的性質。

會用不等式的性質和基本不等式  a² ≥0(a∈R)   a²+b²≥2ab(a、b∈R)、 a+b≥2√ab （a、b≥0）解決一些簡單問題。

1. 會解一元一次不等式，一元一次不等式組和可化為一元一次不等式組的不等式，會解一元二次不等式，了解區間的概念，會在數軸上表示不等式或不等式組的解集。

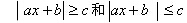3、了解絕對值不等式的性質，會解形如的絕對值不等式。
   （三）數列

1. 了解數列及其有關概念。
2. 理解等差數列、等差中項的概念，會靈活運用等差數列的通項公式、前n項和公式解決有關問題。
3. 理解等比數列，等比中項的概念，會用等比數列的通項公式、前n項和公式解決有關問題。

（四）復數
1、理解復數與復平面的有關概念，會用向量表示復數。
2、了解復數的三角形式，會進行復數的代數形式與三角形式的互化。
3、會進行復數的代數形式的加、減、乘、除運算，會進行復數的三角形式的乘、除、乘方、開方運算。
4、會在復數集中解實系數一元二次方程。
（五）導數
1、了解函數極限的概念，了解函數極限的四則運算法則，了解函數連續的意義。
2、理解導數的概念及其幾何意義。
3、會用基本導數公式（c, x^m(m為有理數)，e^x, lnx的導數），掌握兩個函數和、差、積、商的求導法則。
4、理解極大值、極少值、最大值、最小值的概念，并運用導數求有關函數的單調區間、極大值、極少值及閉區間上的最大值和最小值。
5、會求有關曲線的切線方程，會用導數求簡單實際問題的最大值和最小值。
 
第二部分 三角
（一）三角函數及其有關概念
1、了解正角、負角、零角的概念，理解象限角和終邊相同的角的概念。
2、理解弧度的概念，會進行弧度與角度的換算。
3、理解任意角三角函數的概念。識記三角函數在各象限的符號和特殊角的三角函數值。
（二）三角函數式的變換
1、掌握同角三角函數間的基本關系式，誘導公式，會用它們進行計算、化簡和證明。
2、掌握兩角和、兩角差、二倍角的正弦、余弦、正切的公式，會用它們進行計算、化簡和證明。
（三）三角函數的圖像和性質
1、掌握正弦函數，余弦函數的圖像和性質，會用這兩個函數的性質（定義域、值域、周期性、奇偶性和單調性）解決有關問題。
2、了解正切函數的圖像和性質。
3、了解函數y＝Asin x y ＝sin(χ+φ) 、 y＝sin ωχ、 y＝Asin(ωχ+ φ ) 與 y＝sin χ 的圖像之間的關系，會用“五點法”畫出它們的簡圖，會求函數y＝Asin(ωχ+φ)的周期、最大值和最小值。
4、會由已知三角函數值求角，并會用符號 arcsin χ、arccos χ、arctan χ 表示。
（四）解三角形
1、掌握直角三角形的邊角關系，會用它們解直角三角形及應用題。
2、掌握正弦定理、余弦定理，會用它們解斜三角形及簡單應用題，會根據三角形兩邊及其夾角求三角形的面積。
  
第三部分 平面解析幾何

• 平面向量
  1. 理解向量的概念，掌握向量的幾何表示，了解共線向量的概念。
  2. 掌握向量的加、減法運算。掌握數乘向量的運算。了解兩個向量共線的條件。
  3. 了解平面向量的分解定理。掌握直線的向量參數方程。
  4. 掌握向量數量積運算，了解運算的幾何意義。了解向量數量積運算在處理長度、角度及垂直問題的應用。掌握向量垂直的條件。
  5. 掌握向量的直角坐標及其運算。

6、掌握平面內兩點間的距離公式、線段的中點公式和平移公式。

• 直線
  1. 理解直線的傾斜角和斜率的概念，會求直線的斜率。
  2. 會求直線方程，能靈活運用直線方程解決有關問題。                    

3、掌握兩條直線平行與垂直的條件以及點到直線的距離公式，會用它們解決有關問題。了解兩直線所成角的公式。

• 圓錐曲線
  1. 了解曲線和方程的關系，會求兩條曲線的交點。
  2. 了解充分條件、必要條件、充分必要條件的概念。
  3. 掌握圓的標準方程和一般方程以及直線與圓的位置關系，能靈活運用它們解決有關問題。
  4. 理解橢圓、雙曲線、拋物線的概念，掌握它們的標準方程和性質，能靈活運用他們解決有關問題。
  5. 了解坐標軸的平移公式，會用平移公式化簡圓錐曲線方程。

6、了解參數方程的概念、理解圓和橢圓的參數方程。
第四部分 立體幾何
（一）直線和平面
1、了解平面的基本性質。
2、了解空間兩條直線的位置關系以及異面直線所成角的概念。
3、了解空間直線和平面的位置關系。了解直線和平面垂直的概念，點到平面距離的概念。理解直線和平面平行、垂直的判定定理和性質定理。
4、了解點、斜線和斜線段在平面內射影、直線和平面所成角的概念。了解三垂線定理及其逆定理。
5、了解空間兩個平面的位置關系以及二面角、二面角的平面角、兩平行平面距離的概念。了解兩平面平行、垂直的判定定理和性質定理。
    （二）空間向量
1、了解空間向量的概念、掌握空間向量的加法、減法和數乘向量的運算。掌握向量平移。
2、解空間向量分解定理。理解直線的方向向量。掌握直線的向量參數方程。
3、掌握空間數量積的定義及其運算。
4、會用向量運解決空間中的平行、垂直、夾角和距離等簡單幾何問題。
（三）多面體和旋轉體

1. 了解直棱柱、正棱柱和平行六面體的概念，性質，會計算它們的表面積和體積。
2. 解棱錐、正棱錐的概念、性質，會計算它們的表面積和體積。
3. 了解圓柱、圓錐的概念，性質，會計算它們的表面積和體積。
4. 解球的概念、性質，會計算球面面積和球體體積。

第五部分 概率與統計初步
（一）排列、組合和二項式定理
1、了解分類計算原理和分步計數原理。
2、會解排列、組合的意義，掌握排列數、組合數的計算公式。
3、會解排列、組合的簡單應用題。
4、了解二項式定理、會用二項展開式的性質和通項公式解決簡單問題。
    （二）概率與統計初步
1、了解隨機事件及其概率的意義。
2、了解等可能性事件的概率的意義，會用計算方法和排列組合基本公式計算一些等可能性事件的概率。
3、了解互斥事件的意義，會用互斥事件的概率加法公式計算一些事件的概率。
4、了解相互獨立事件的意義，會用相互獨立事件的概率乘法公式計算一些事件的概率。
5、會計算事件在n 次獨立重復試驗中恰好發生r 次的概率。
6、了解總體和樣本的概念，會計算樣本平均數和樣本方差。
7、了解離散型隨機變量及其期望的意義，會根據離散型隨機變量的分布列求出期望值。
8、了解線性回歸的方法極其簡單應用。

• 考試形式及試卷結構

考試形式
閉卷，筆答。
全卷滿分為100分，考試時間為120分鐘。
   試卷結構

• 試卷內容比例  

代數 約40％      三角 約15％     平面解析幾何 約20％ 
立體幾何 15％    概率與統計約 10％

• 題型比例   

選擇題 約50％    填空題 約10％   解答題（包括證明題） 約40％

• 試題難易比例 

較容易題 約30％  中等難度題  約50％  較難題 約20％